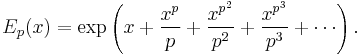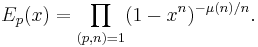Artin–Hasse exponential

In mathematics, the Artin–Hasse exponential, named after Emil Artin and Helmut Hasse, is the power series given by

$E_p(x) = \exp\left(x %2B \frac{x^p}{p} %2B \frac{x^{p^2}}{p^2} %2B \frac{x^{p^3}}{p^3} %2B\cdots\right).$

Properties

The coefficients are p-integral; in other words, their denominators are not divisible by p. This follows from Dwork's lemma, which says that a power series f(x) = 1 + ... with rational coefficients has p-integral coefficients if and only if f(x^p)/f(x)^p ≡ 1 mod p.
The coefficient of xⁿ of n! E_p(x) is the number of elements of the symmetric group on n points of order a power of p. (This gives another proof that the coefficients are p-integral, using the fact that in a finite group of order divisible by d the number of elements of order dividing d is also divisible by d.)
It can be written as the infinite product

$E_p(x) = \prod_{(p,n)=1}(1-x^n)^{-\mu(n)/n}.$

(The function μ is the Möbius function.) This resembles the exponential series, in the sense that taking this product over all n rather than only n prime to p is an infinite product which converges (in the ring of formal power series) to the exponential series.

References

A course in p-adic analysis, by Alain M. Robert
Fesenko, Ivan B.; Vostokov, Sergei V. (2002), Local fields and their extensions, Translations of Mathematical Monographs, 121 (Second ed.), Providence, RI: American Mathematical Society, ISBN 9780821832592, MR 1915966

Artin–Hasse exponential

Properties

See also

References